| tags: [ Data Cleaning Imputation PCA R ] categories: [Coding Experiments ]
MIPCA of Phenotypic Data without LogMAR-with-PH values
# required packages
require(tidyverse)
require(broom)
require(missMDA)
require(FactoMineR)
require(moments)
require(Hmisc)
require(corrplot)Introduction
After adding in additional variables, which included logMAR and base-out prism test values, the variable factor plots indicated that there was a large uncertainty around the imputed values of the logMAR with pinhole correction values. Therefore, the right and left pinhole correction variables (LVA and RVA with PH).
Methods and Results
1. Subset quantitative variables excluding LVA and RVA with PH variables.
phen.data.age<- read.csv('C:/Users/Martha/Documents/Honours/Project/honours.project/Data/NIES_master_database-age.csv')
phen.data.adults<-phen.data.age[phen.data.age$Age.excel>17,]
quant.variables<- c("Logmar.VA.Right", "Logmar.VA.Left", "R.Sph..pre.dilate.", "R.Cyl..pre.dilate.",
"R.Axis..pre.dilate.", "L.Sph..pre.dilate.", "L.Cyl..pre.dilate.", "L.Axis..pre.dilate.",
"R.K.value.H", "R.K.Value.H.Axis", "R.K.value.V", "R.K.value.V.Axis", "L.K.value.H",
"L.K.value.H.Axis", "L.K.value.V", "L.K.value.V.Axis", "R.Pachimetry", "L.Pachimetry",
"R.Axial.Length","L.Axial.Length", "AC.Depth.R", "AC.Depth.L", "R.IOP.mmHg", "L.IOP.mmHg",
"CDR.RE", "CDR.LE")
quant.data.adults<- phen.data.adults[quant.variables]
summary(quant.data.adults)## Logmar.VA.Right Logmar.VA.Left R.Sph..pre.dilate.
## Min. :-0.30000 Min. :-0.30000 Min. :-8.0000
## 1st Qu.:-0.08000 1st Qu.:-0.10000 1st Qu.: 0.0000
## Median : 0.02000 Median : 0.02000 Median : 0.5000
## Mean : 0.06608 Mean : 0.06359 Mean : 0.5455
## 3rd Qu.: 0.14000 3rd Qu.: 0.13000 3rd Qu.: 1.2500
## Max. : 2.00000 Max. : 1.70000 Max. : 8.5000
## NA's :3 NA's :6 NA's :10
## R.Cyl..pre.dilate. R.Axis..pre.dilate. L.Sph..pre.dilate.
## Min. :-11.0000 Min. : 0.00 Min. :-9.5000
## 1st Qu.: -0.7500 1st Qu.: 25.50 1st Qu.: 0.0000
## Median : -0.5000 Median : 85.00 Median : 0.5000
## Mean : -0.6497 Mean : 80.23 Mean : 0.5887
## 3rd Qu.: -0.2500 3rd Qu.:119.00 3rd Qu.: 1.2500
## Max. : 0.0000 Max. :180.00 Max. : 8.0000
## NA's :10 NA's :10 NA's :9
## L.Cyl..pre.dilate. L.Axis..pre.dilate. R.K.value.H R.K.Value.H.Axis
## Min. :-9.7500 Min. : 0.00 Min. :36.00 Min. : 0.00
## 1st Qu.:-0.7500 1st Qu.: 13.00 1st Qu.:42.00 1st Qu.: 42.00
## Median :-0.5000 Median : 70.00 Median :43.00 Median : 91.00
## Mean :-0.6522 Mean : 72.25 Mean :42.97 Mean : 93.74
## 3rd Qu.:-0.2500 3rd Qu.:113.00 3rd Qu.:44.00 3rd Qu.:156.00
## Max. : 0.0000 Max. :180.00 Max. :48.25 Max. :180.00
## NA's :9 NA's :9 NA's :16 NA's :16
## R.K.value.V R.K.value.V.Axis L.K.value.H L.K.value.H.Axis
## Min. :37.00 Min. : 1.00 Min. :32.75 Min. : 0.0
## 1st Qu.:42.75 1st Qu.: 62.00 1st Qu.:42.00 1st Qu.: 24.0
## Median :43.75 Median : 89.00 Median :43.00 Median : 88.5
## Mean :43.80 Mean : 91.18 Mean :42.97 Mean : 87.8
## 3rd Qu.:45.00 3rd Qu.:127.00 3rd Qu.:44.00 3rd Qu.:147.0
## Max. :55.00 Max. :180.00 Max. :47.25 Max. :180.0
## NA's :16 NA's :16 NA's :15 NA's :15
## L.K.value.V L.K.value.V.Axis R.Pachimetry L.Pachimetry
## Min. :39.00 Min. : 0.00 Min. :428.0 Min. :424.0
## 1st Qu.:42.81 1st Qu.: 65.25 1st Qu.:527.0 1st Qu.:526.0
## Median :43.75 Median : 90.00 Median :546.0 Median :547.0
## Mean :43.87 Mean : 92.22 Mean :546.2 Mean :546.3
## 3rd Qu.:44.75 3rd Qu.:119.75 3rd Qu.:570.0 3rd Qu.:568.0
## Max. :52.00 Max. :180.00 Max. :656.0 Max. :658.0
## NA's :15 NA's :15 NA's :14 NA's :16
## R.Axial.Length L.Axial.Length AC.Depth.R AC.Depth.L
## Min. :20.95 Min. :21.29 Min. :2.090 Min. :2.000
## 1st Qu.:22.90 1st Qu.:22.87 1st Qu.:3.058 1st Qu.:3.040
## Median :23.50 Median :23.46 Median :3.310 Median :3.280
## Mean :23.56 Mean :23.54 Mean :3.320 Mean :3.306
## 3rd Qu.:24.09 3rd Qu.:24.11 3rd Qu.:3.550 3rd Qu.:3.553
## Max. :27.66 Max. :34.43 Max. :4.950 Max. :5.130
## NA's :13 NA's :13 NA's :13 NA's :13
## R.IOP.mmHg L.IOP.mmHg CDR.RE CDR.LE
## Min. : 6.00 Min. : 8.00 Min. :0.0000 Min. :0.0000
## 1st Qu.:14.00 1st Qu.:14.00 1st Qu.:0.3000 1st Qu.:0.3000
## Median :16.00 Median :16.00 Median :0.4000 Median :0.4000
## Mean :15.88 Mean :16.06 Mean :0.4057 Mean :0.4022
## 3rd Qu.:18.00 3rd Qu.:18.00 3rd Qu.:0.5000 3rd Qu.:0.5000
## Max. :28.00 Max. :33.00 Max. :0.9900 Max. :0.9000
## NA's :2 NA's :3 NA's :19 NA's :172. Duplicate subset of data and force into a matrix
ocular_data <- quant.data.adults
ocular_data <- as.matrix(ocular_data)3. Run multiple PCA imputation
nbdim = estim_ncpPCA(ocular_data, method = 'EM', method.cv="Kfold")##
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|=== | 4%
|
|=== | 5%
|
|==== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======= | 11%
|
|======== | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 15%
|
|=========== | 16%
|
|=========== | 17%
|
|============ | 18%
|
|============ | 19%
|
|============= | 20%
|
|============== | 21%
|
|============== | 22%
|
|=============== | 23%
|
|================ | 24%
|
|================ | 25%
|
|================= | 26%
|
|================== | 27%
|
|================== | 28%
|
|=================== | 29%
|
|==================== | 30%
|
|==================== | 31%
|
|===================== | 32%
|
|====================== | 33%
|
|====================== | 34%
|
|======================= | 35%
|
|======================== | 36%
|
|======================== | 37%
|
|========================= | 38%
|
|========================== | 39%
|
|========================== | 40%
|
|=========================== | 41%
|
|============================ | 42%
|
|============================ | 43%
|
|============================= | 44%
|
|============================== | 45%
|
|============================== | 46%
|
|=============================== | 47%
|
|================================ | 48%
|
|================================ | 49%
|
|================================= | 51%
|
|================================= | 52%
|
|================================== | 53%
|
|=================================== | 54%
|
|=================================== | 55%
|
|==================================== | 56%
|
|===================================== | 57%
|
|===================================== | 58%
|
|====================================== | 59%
|
|======================================= | 60%
|
|======================================= | 61%
|
|======================================== | 62%
|
|========================================= | 63%
|
|========================================= | 64%
|
|========================================== | 65%
|
|=========================================== | 66%
|
|=========================================== | 67%
|
|============================================ | 68%
|
|============================================= | 69%
|
|============================================= | 70%
|
|============================================== | 71%
|
|=============================================== | 72%
|
|=============================================== | 73%
|
|================================================ | 74%
|
|================================================= | 75%
|
|================================================= | 76%
|
|================================================== | 77%
|
|=================================================== | 78%
|
|=================================================== | 79%
|
|==================================================== | 80%
|
|===================================================== | 81%
|
|===================================================== | 82%
|
|====================================================== | 83%
|
|====================================================== | 84%
|
|======================================================= | 85%
|
|======================================================== | 86%
|
|======================================================== | 87%
|
|========================================================= | 88%
|
|========================================================== | 89%
|
|========================================================== | 90%
|
|=========================================================== | 91%
|
|============================================================ | 92%
|
|============================================================ | 93%
|
|============================================================= | 94%
|
|============================================================== | 95%
|
|============================================================== | 96%
|
|=============================================================== | 97%
|
|================================================================ | 98%
|
|================================================================ | 99%
|
|=================================================================| 100%nbdim## $ncp
## [1] 5
##
## $criterion
## 0 1 2 3 4 5
## 807347.2 809277.1 805498.0 805007.5 798120.2 786467.2res.comp = MIPCA(ocular_data, ncp = nbdim$ncp, nboot = 1000)
png('indiv_plot_2.png', width = 3200, height = 3200, res = 150)
plot.MIPCA(res.comp, choice = "ind.supp")
dev.off()## png
## 2png('var_plot_2.png', width = 3200, height = 3200, res = 150)
plot.MIPCA(res.comp, choice = "var")
dev.off()## png
## 24. Run summary and distribution statistics post-imputation
imputed_phen_data<-res.comp$res.imputePCA
head(imputed_phen_data)## Logmar.VA.Right Logmar.VA.Left R.Sph..pre.dilate. R.Cyl..pre.dilate.
## 1 0.02 -0.04 0.25 0.00
## 2 0.10 0.16 0.00 -0.75
## 3 0.00 0.00 1.25 -1.25
## 4 0.30 0.08 1.25 -0.25
## 5 0.00 -0.10 1.25 -0.25
## 6 0.24 0.36 4.00 -0.50
## R.Axis..pre.dilate. L.Sph..pre.dilate. L.Cyl..pre.dilate.
## 1 0 0.25 -0.50
## 2 28 -0.50 -0.25
## 3 148 1.25 -0.25
## 4 97 1.50 -0.50
## 5 37 1.25 -0.75
## 6 46 3.75 -0.75
## L.Axis..pre.dilate. R.K.value.H R.K.Value.H.Axis R.K.value.V
## 1 79 42.00000 2.0000 43.00000
## 2 164 41.25000 7.0000 42.25000
## 3 24 43.77619 147.5682 44.76719
## 4 81 44.75000 5.0000 45.00000
## 5 164 44.75000 0.0000 44.75000
## 6 180 42.00000 8.0000 43.25000
## R.K.value.V.Axis L.K.value.H L.K.value.H.Axis L.K.value.V
## 1 92.00000 42.50000 5.00000 43.50000
## 2 97.00000 41.50000 168.00000 42.00000
## 3 48.29713 43.92883 36.60368 44.74071
## 4 95.00000 45.00000 60.00000 45.25000
## 5 90.00000 44.25000 178.00000 44.75000
## 6 98.00000 42.25000 177.00000 43.25000
## L.K.value.V.Axis R.Pachimetry L.Pachimetry R.Axial.Length L.Axial.Length
## 1 95.0000 532 554 24.31 24.10
## 2 78.0000 608 612 25.02 25.21
## 3 138.2271 507 510 22.78 22.80
## 4 150.0000 560 559 23.02 22.98
## 5 88.0000 556 562 21.75 22.04
## 6 87.0000 498 501 23.06 23.17
## AC.Depth.R AC.Depth.L R.IOP.mmHg L.IOP.mmHg CDR.RE CDR.LE
## 1 3.09 3.03 14 14 0.9 0.9
## 2 3.38 3.92 16 15 0.9 0.7
## 3 3.40 3.45 26 22 0.7 0.7
## 4 3.00 2.85 14 14 0.2 0.2
## 5 2.60 2.53 22 21 0.3 0.3
## 6 2.94 3.04 18 20 0.6 0.6summary_stats_imputed <-summary(imputed_phen_data)
summary_stats_imputed## Logmar.VA.Right Logmar.VA.Left R.Sph..pre.dilate.
## Min. :-0.30000 Min. :-0.30000 Min. :-8.0000
## 1st Qu.:-0.08000 1st Qu.:-0.10000 1st Qu.: 0.0000
## Median : 0.02000 Median : 0.02000 Median : 0.5000
## Mean : 0.06624 Mean : 0.06451 Mean : 0.5477
## 3rd Qu.: 0.14000 3rd Qu.: 0.14000 3rd Qu.: 1.2500
## Max. : 2.00000 Max. : 1.70000 Max. : 8.5000
## R.Cyl..pre.dilate. R.Axis..pre.dilate. L.Sph..pre.dilate.
## Min. :-11.0000 Min. : 0.00 Min. :-9.5000
## 1st Qu.: -0.7500 1st Qu.: 26.00 1st Qu.: 0.0000
## Median : -0.5000 Median : 85.00 Median : 0.5000
## Mean : -0.6542 Mean : 80.25 Mean : 0.5938
## 3rd Qu.: -0.2500 3rd Qu.:118.00 3rd Qu.: 1.2500
## Max. : 0.0000 Max. :180.00 Max. : 8.0000
## L.Cyl..pre.dilate. L.Axis..pre.dilate. R.K.value.H R.K.Value.H.Axis
## Min. :-9.7500 Min. : 0.00 Min. :36.00 Min. : 0.00
## 1st Qu.:-0.7500 1st Qu.: 14.00 1st Qu.:42.00 1st Qu.: 44.00
## Median :-0.5000 Median : 72.00 Median :43.00 Median : 92.00
## Mean :-0.6572 Mean : 72.44 Mean :42.96 Mean : 93.86
## 3rd Qu.:-0.2500 3rd Qu.:112.00 3rd Qu.:44.00 3rd Qu.:154.00
## Max. : 0.0000 Max. :180.00 Max. :48.25 Max. :180.00
## R.K.value.V R.K.value.V.Axis L.K.value.H L.K.value.H.Axis
## Min. :37.00 Min. : 1.00 Min. :32.75 Min. : 0.00
## 1st Qu.:42.75 1st Qu.: 63.00 1st Qu.:42.00 1st Qu.: 26.00
## Median :43.75 Median : 89.00 Median :43.00 Median : 88.00
## Mean :43.80 Mean : 91.07 Mean :42.96 Mean : 87.76
## 3rd Qu.:44.77 3rd Qu.:124.00 3rd Qu.:44.00 3rd Qu.:145.00
## Max. :55.00 Max. :180.00 Max. :47.25 Max. :180.00
## L.K.value.V L.K.value.V.Axis R.Pachimetry L.Pachimetry
## Min. :39.00 Min. : 0.0 Min. :428 Min. :424.0
## 1st Qu.:42.88 1st Qu.: 68.0 1st Qu.:526 1st Qu.:526.0
## Median :43.75 Median : 90.0 Median :546 Median :547.0
## Mean :43.87 Mean : 92.3 Mean :546 Mean :546.1
## 3rd Qu.:44.75 3rd Qu.:119.0 3rd Qu.:569 3rd Qu.:568.0
## Max. :52.00 Max. :180.0 Max. :656 Max. :658.0
## R.Axial.Length L.Axial.Length AC.Depth.R AC.Depth.L
## Min. :20.95 Min. :21.29 Min. :2.090 Min. :2.000
## 1st Qu.:22.91 1st Qu.:22.87 1st Qu.:3.060 1st Qu.:3.040
## Median :23.51 Median :23.47 Median :3.310 Median :3.290
## Mean :23.56 Mean :23.54 Mean :3.322 Mean :3.308
## 3rd Qu.:24.10 3rd Qu.:24.11 3rd Qu.:3.560 3rd Qu.:3.560
## Max. :27.66 Max. :34.43 Max. :4.950 Max. :5.130
## R.IOP.mmHg L.IOP.mmHg CDR.RE CDR.LE
## Min. : 6.00 Min. : 8.00 Min. :0.0000 Min. :0.0000
## 1st Qu.:14.00 1st Qu.:14.00 1st Qu.:0.3000 1st Qu.:0.3000
## Median :16.00 Median :16.00 Median :0.4000 Median :0.4000
## Mean :15.88 Mean :16.06 Mean :0.4077 Mean :0.4039
## 3rd Qu.:18.00 3rd Qu.:18.00 3rd Qu.:0.5000 3rd Qu.:0.5000
## Max. :28.00 Max. :33.00 Max. :0.9900 Max. :0.90005. Plot histograms of imputed data
imputed_phen_data %>%
as.data.frame %>%
keep(is.numeric) %>%
gather() %>%
ggplot(aes(value)) + facet_wrap(~ key, scales = "free") + geom_histogram(fill = 'grey', colour = "black")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.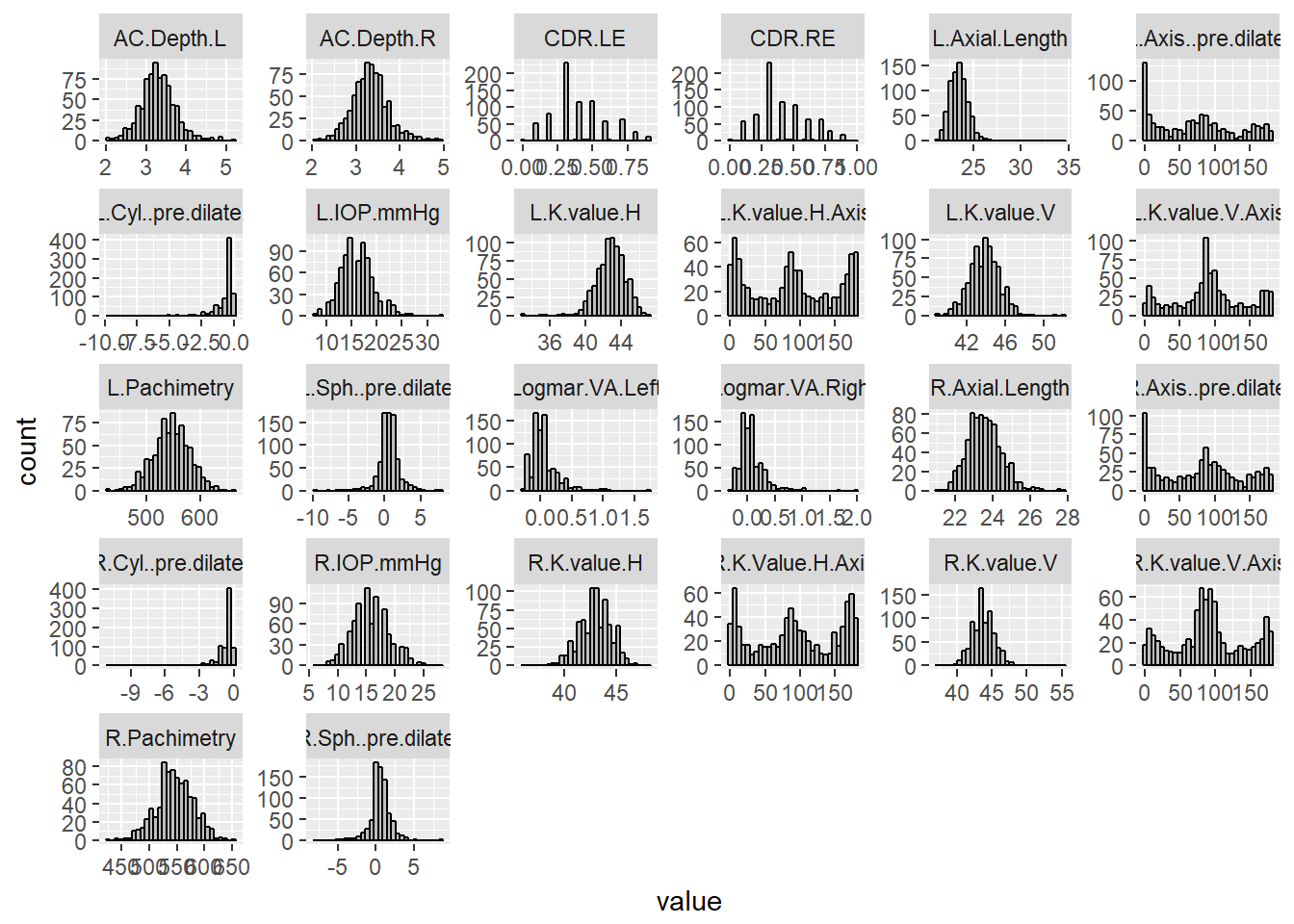
6. Find skewness and kurtosis of imputed data
skewness_imp<-skewness(imputed_phen_data)
kurtosis_imp<-kurtosis(imputed_phen_data)
sum_skew_kurt_stats<-rbind(summary_stats_imputed, skewness_imp, kurtosis_imp)
sum_skew_kurt_stats## Logmar.VA.Right Logmar.VA.Left
## "Min. :-0.30000 " "Min. :-0.30000 "
## "1st Qu.:-0.08000 " "1st Qu.:-0.10000 "
## "Median : 0.02000 " "Median : 0.02000 "
## "Mean : 0.06624 " "Mean : 0.06451 "
## "3rd Qu.: 0.14000 " "3rd Qu.: 0.14000 "
## "Max. : 2.00000 " "Max. : 1.70000 "
## skewness_imp "2.59213925781422" "1.9858399104377"
## kurtosis_imp "15.6535529988487" "9.79308760942436"
## R.Sph..pre.dilate. R.Cyl..pre.dilate.
## "Min. :-8.0000 " "Min. :-11.0000 "
## "1st Qu.: 0.0000 " "1st Qu.: -0.7500 "
## "Median : 0.5000 " "Median : -0.5000 "
## "Mean : 0.5477 " "Mean : -0.6542 "
## "3rd Qu.: 1.2500 " "3rd Qu.: -0.2500 "
## "Max. : 8.5000 " "Max. : 0.0000 "
## skewness_imp "-0.496979099960277" "-5.06776895408613"
## kurtosis_imp "9.82563682016026" "50.4636709556355"
## R.Axis..pre.dilate. L.Sph..pre.dilate. L.Cyl..pre.dilate.
## "Min. : 0.00 " "Min. :-9.5000 " "Min. :-9.7500 "
## "1st Qu.: 26.00 " "1st Qu.: 0.0000 " "1st Qu.:-0.7500 "
## "Median : 85.00 " "Median : 0.5000 " "Median :-0.5000 "
## "Mean : 80.25 " "Mean : 0.5938 " "Mean :-0.6572 "
## "3rd Qu.:118.00 " "3rd Qu.: 1.2500 " "3rd Qu.:-0.2500 "
## "Max. :180.00 " "Max. : 8.0000 " "Max. : 0.0000 "
## skewness_imp "0.0676297008960507" "-0.702742368467331" "-4.73466819820079"
## kurtosis_imp "1.90089128041046" "10.4640526005827" "35.5700850187859"
## L.Axis..pre.dilate. R.K.value.H R.K.Value.H.Axis
## "Min. : 0.00 " "Min. :36.00 " "Min. : 0.00 "
## "1st Qu.: 14.00 " "1st Qu.:42.00 " "1st Qu.: 44.00 "
## "Median : 72.00 " "Median :43.00 " "Median : 92.00 "
## "Mean : 72.44 " "Mean :42.96 " "Mean : 93.86 "
## "3rd Qu.:112.00 " "3rd Qu.:44.00 " "3rd Qu.:154.00 "
## "Max. :180.00 " "Max. :48.25 " "Max. :180.00 "
## skewness_imp "0.298060949039886" "-0.329380707180307" "-0.086835172184765"
## kurtosis_imp "1.88816243797929" "3.66766428468599" "1.72958520888624"
## R.K.value.V R.K.value.V.Axis L.K.value.H
## "Min. :37.00 " "Min. : 1.00 " "Min. :32.75 "
## "1st Qu.:42.75 " "1st Qu.: 63.00 " "1st Qu.:42.00 "
## "Median :43.75 " "Median : 89.00 " "Median :43.00 "
## "Mean :43.80 " "Mean : 91.07 " "Mean :42.96 "
## "3rd Qu.:44.77 " "3rd Qu.:124.00 " "3rd Qu.:44.00 "
## "Max. :55.00 " "Max. :180.00 " "Max. :47.25 "
## skewness_imp "0.43233098223396" "0.0453466088684528" "-0.938227281325446"
## kurtosis_imp "6.27962328259508" "2.29020773340462" "6.95195691414879"
## L.K.value.H.Axis L.K.value.V
## "Min. : 0.00 " "Min. :39.00 "
## "1st Qu.: 26.00 " "1st Qu.:42.88 "
## "Median : 88.00 " "Median :43.75 "
## "Mean : 87.76 " "Mean :43.87 "
## "3rd Qu.:145.00 " "3rd Qu.:44.75 "
## "Max. :180.00 " "Max. :52.00 "
## skewness_imp "0.0561687602827247" "0.230213726384767"
## kurtosis_imp "1.69477477774781" "4.10550830623158"
## L.K.value.V.Axis R.Pachimetry
## "Min. : 0.0 " "Min. :428 "
## "1st Qu.: 68.0 " "1st Qu.:526 "
## "Median : 90.0 " "Median :546 "
## "Mean : 92.3 " "Mean :546 "
## "3rd Qu.:119.0 " "3rd Qu.:569 "
## "Max. :180.0 " "Max. :656 "
## skewness_imp "-0.0260547158131096" "-0.129162958803714"
## kurtosis_imp "2.3872472044967" "3.11054159015654"
## L.Pachimetry R.Axial.Length L.Axial.Length
## "Min. :424.0 " "Min. :20.95 " "Min. :21.29 "
## "1st Qu.:526.0 " "1st Qu.:22.91 " "1st Qu.:22.87 "
## "Median :547.0 " "Median :23.51 " "Median :23.47 "
## "Mean :546.1 " "Mean :23.56 " "Mean :23.54 "
## "3rd Qu.:568.0 " "3rd Qu.:24.10 " "3rd Qu.:24.11 "
## "Max. :658.0 " "Max. :27.66 " "Max. :34.43 "
## skewness_imp "-0.0946336090284606" "0.623525487607831" "2.03281154238147"
## kurtosis_imp "3.24201178838641" "4.20517591208724" "20.6444882646786"
## AC.Depth.R AC.Depth.L R.IOP.mmHg
## "Min. :2.090 " "Min. :2.000 " "Min. : 6.00 "
## "1st Qu.:3.060 " "1st Qu.:3.040 " "1st Qu.:14.00 "
## "Median :3.310 " "Median :3.290 " "Median :16.00 "
## "Mean :3.322 " "Mean :3.308 " "Mean :15.88 "
## "3rd Qu.:3.560 " "3rd Qu.:3.560 " "3rd Qu.:18.00 "
## "Max. :4.950 " "Max. :5.130 " "Max. :28.00 "
## skewness_imp "0.384450222967117" "0.410626913089036" "0.219078586934118"
## kurtosis_imp "3.99826255554454" "4.26858836528065" "3.09283419803348"
## L.IOP.mmHg CDR.RE CDR.LE
## "Min. : 8.00 " "Min. :0.0000 " "Min. :0.0000 "
## "1st Qu.:14.00 " "1st Qu.:0.3000 " "1st Qu.:0.3000 "
## "Median :16.00 " "Median :0.4000 " "Median :0.4000 "
## "Mean :16.06 " "Mean :0.4077 " "Mean :0.4039 "
## "3rd Qu.:18.00 " "3rd Qu.:0.5000 " "3rd Qu.:0.5000 "
## "Max. :33.00 " "Max. :0.9900 " "Max. :0.9000 "
## skewness_imp "0.456553888331421" "0.526448428177066" "0.509487222778446"
## kurtosis_imp "3.91355078592957" "2.74101114433666" "2.74660317565884"Discussion
The data was imputed successfully and produced a complete data set. The histograms of the imputed values show that most variables have a single peak and are relatively normally distributed. The histograms for the axes variables (Left/Right V/H Axis), however, exhibit a trimodal distribution, showing peaks around 0, 90, and 180 degrees. The distribution statistics indicate that the logMAR values (left and right) and left axial length are strongly positively skewed, while the left/right Cryl pre-dilate variables are negatively skewed. Interestingly, the right axial length is only slightly positively skewed (skewness = 0.62).